Em mecânica quântica, a solução da Equação de Schrödinger para o átomo de Hidrogênio é o processo de resolução da equação diferencial parcial formulada por Erwin Schrödinger em 1925. Este caso particular é o de duas partículas de cargas elétricas de mesmo módulo e sinais opostos (um elétron e um próton). Vamos direto ao ponto, este post é puramente matemático. Para maiores detalhes sobre a teoria, veja as postagens anteriores.

Partindo da equação de Schorodinger independente do tempo (ESIT):

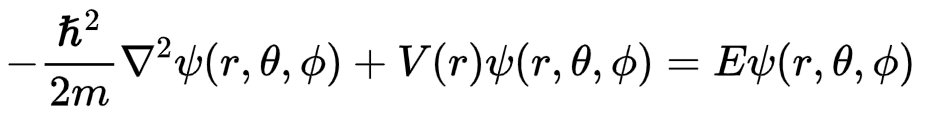
vamos substituir o Laplaciano em coordenadas esféricas (abaixo) na ESIT.

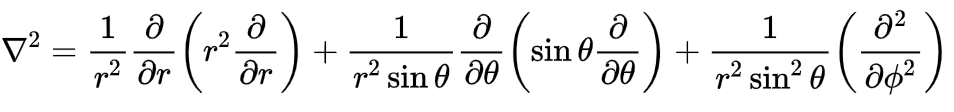
Substituindo o Laplaciano, temos:

Sabendo que a solução da ESIT pode ser escrita em termos de uma parte radial e outra angular, podemos escrever:

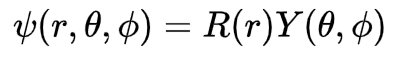
Substituimos esta função na ESIT e rearranjando as derivadas parciais (retirando para fora da derivada termos constantes e permanece dentro da derivada termos que são dependentes) ficamos com:

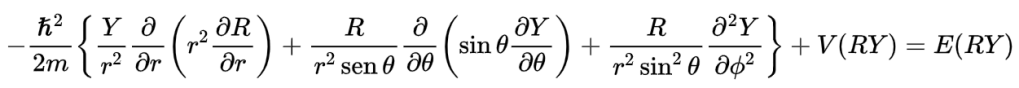
Dividindo a equação acima por R.Y e multiplicando por:

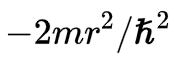
temos,

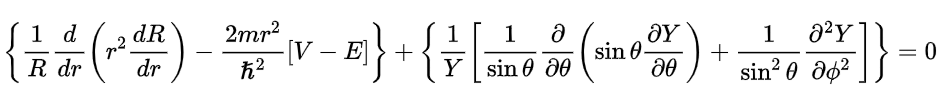
Note que no primeiro termo aparece a derivada da função R(r), logo, temos uma equação diferencial total e não parcial, pois R(r) depende apenas de uma variável (r). No entanto, no segundo termo, aparece a derivada parcial da função Y (θ, Ⴔ) que é função de duas variáveis, logo, temos uma equação diferencial parcial. Nosso objetivo é separar as equações diferenciais parciais em equações diferenciais totais. Para isso, vamos adotar alguns artifícios matemáticos, conforme descrito abaixo:

Aqui podemos nomear o primeiro e o segundo termo da equação como: l(l+1) e – l(l+1) e assim, note que a igualdade continua valendo:

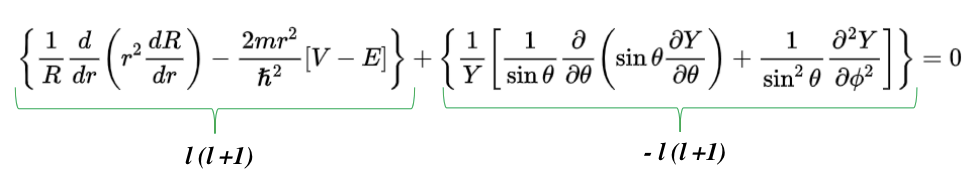
Com esse artificio matemático, é a primeira vez que aparece um dos números quânticos durante a resolução matemática da ESIT.

Vamos manipular agora o segundo termo da equação, reescrito abaixo:

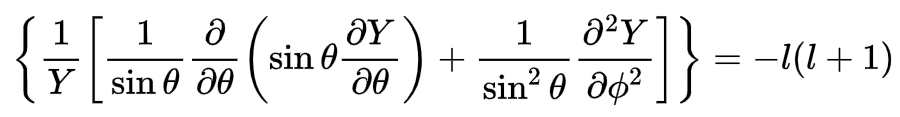
Para separarmos a parte angular em duas funções, vamos substituir Y (θ, Ⴔ), por:

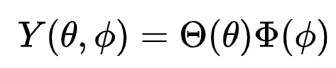
e ao mesmo tempo dividir por Θ.Ø. Ficamos com:

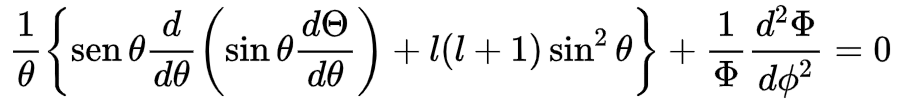
Da mesma forma feita anteriormente, podemos nomear o primeiro e o segundo termo da equação como: + m² e – m² e assim, note que a igualdade continua valendo:

Note que acima, aparece um segundo número quântico ”m”.

Desta forma, ficamos com três equações diferenciais totais e não mais parciais a serem resolvidas. Como já temos a solução de cada uma delas tabeladas, vamos usar essas soluções prontas, pois deriva-las se torna muito complexo. Na tabela abaixo apresentamos as equações diferenciais totais obtidas e suas respectivas soluções (tabeladas), bem como, algumas funções e polinômios tabelados que também são usados nas soluções.

_{Fontes: David J. Griffiths, Introduction to Quantum Mechanics, Pearson Prentice Hall; 2nd edition (2004). Robert Eisberg, Física Quântica – Átomos, Moléculas, Sólidos, Núcleos e Partículas, 1º edição (1979).}